David Abel

Portrait

Plasticity as the Mirror of Empowerment

November 26, 2025

Scientifically, we're still building out our basic understanding of what agents really are: how to define, theorize, and form basic scientific explanations and predictions about them. My research agenda (along with many other great folks!) explores the foundations of agents under lightweight assumptions: Today I'm really excited to share this post covering our new NeurIPS paper, Plasticity as the Mirror of Empowerment, that studies push-and-pull relationship of an agent with its environment under minimal assumptions. In one sentence:

We propose an agent-centric measure for plasticity (the capacity to adapt), and prove that agents can face a fundamental tension between their plasticity and their empowerment (the capacity to steer).

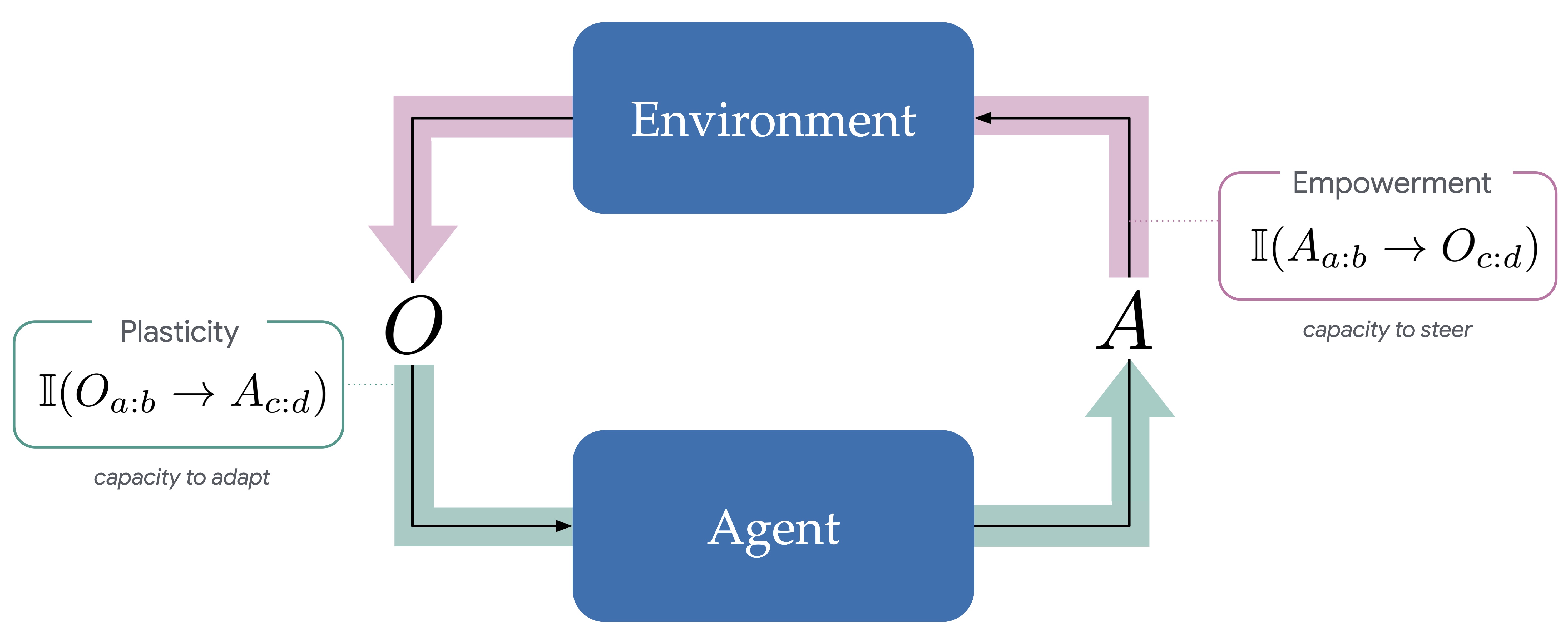
These two capacitys (plasticity=capacity to adapt, empowerment=capacity to steer), are fundamental to agency. If an input-output system cannot adapt, it is just "pushing", and if it cannot steer, it is just absorbing. The really beautiful, mysterious, and powerful thing about an agent is that it can do both. And doing both somehow vastly excedes the capacity to only do one. In this paper, we give a lightweight theoretical foundation for thinking about these two concepts, and prove a new sort of "conservation law" that connects them.

Overview. To see where this conservation comes from, we'll first build an intuitive feel for plasticity and empowerment as concepts. Plasticity is roughly an agent's capacity to adapt to its experience, and empowerment is roughly an agent's capacity to influence its future experience. The main technical work is then to formalise both properties in a suitably general mathematical form, borrowing from the existing rich landscape of work that first proposed empowerment by Klyubin et al.. Like Klyubin's definition of empowerment, we'll use the tools of information theory to defined plasticity based on a new kind of information we call the generalized directed information (GDI).

Using this formalism, we can then state our main result: for any agent, plasticity and empowerment can be in tension. That is, an agent that fully controls its world cannot also be surprised by it. We suggest that this tension may have significant implications for our future understanding and design of reliable, safe, and cooperative agents.

I'll close with some reflections on the research process, some anecdotes that led to the results, a few broader thoughts on conceptual research, and a list of some relevant papers if you want to read more in the area. Here's a little overview:

Let's dive in!

1. What is Plasticity, and What is Empowerment? (top)

Both plasticity and empowerment have been studied across a number of disciplines, with plasticity getting more attention outside of AI, while empowerment has predominantly been an AI-centric concept.

Plasticity

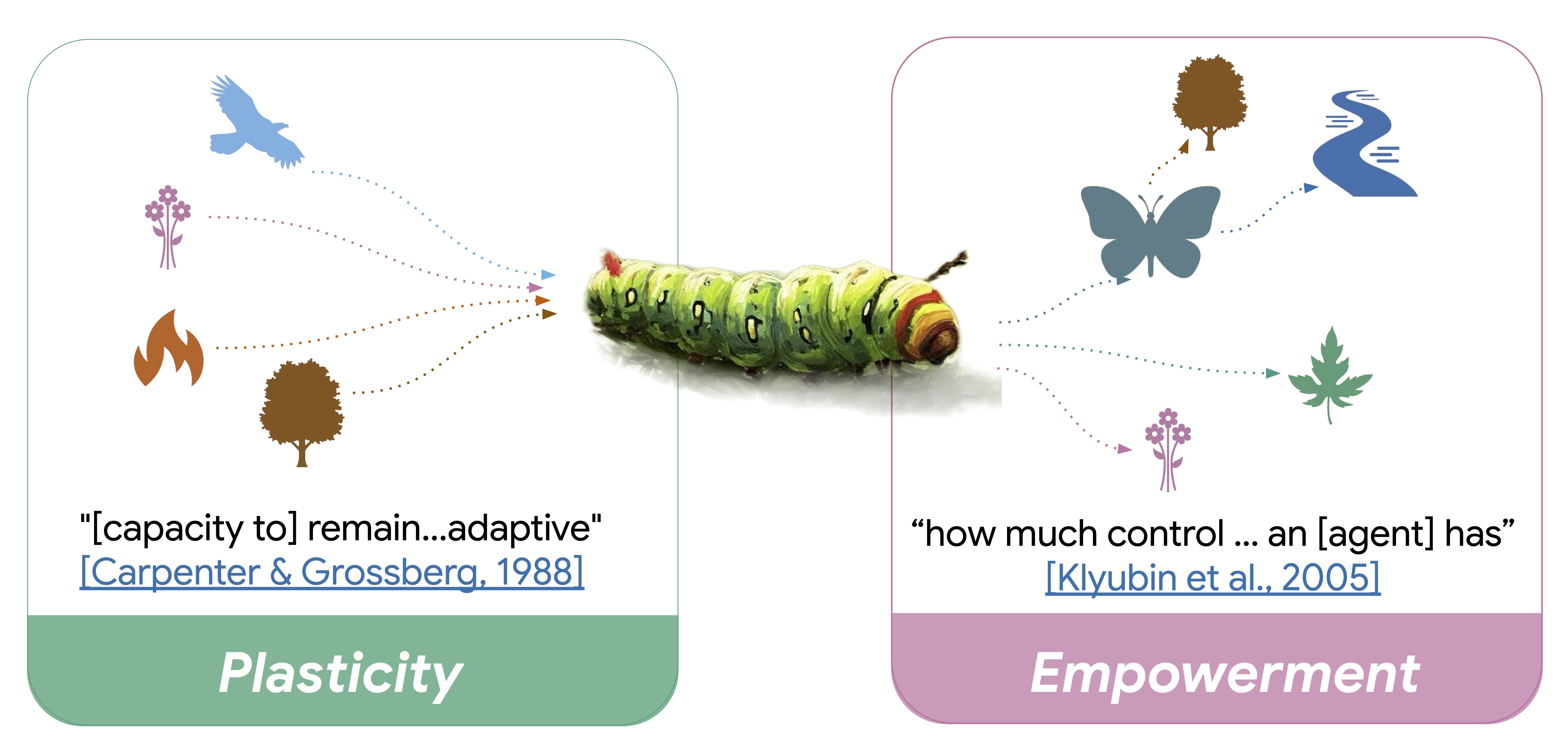
Plasticity is central to a number of fields, including biology, neuroscience, and more recently, machine learning. To my knowledge, the term originates from William James in his 1890 book The Principles of Psychology: "Plasticity ... means the possession of a structure weak enough to yield to an influence, but strong enough not to yield all at once" (Chapter IV). In biology, the study of plasticity shows up shortly after in a 1910 book on ants by Wheeler, who defines the plasticity of an organism as roughly "the power of an organism to adapt action" (p. 531). In this way, plasticity is thought to be a degree of malleability of an organism. Neuroscience primarily views plasticity in terms of neuroplasticity or synaptic plasticity, reflecting the extent to which neural circuity can be rewired in response to stimuli. More recently, in machine learning, plasticity has been studied under the lens of the loss of plasticity of a neural network (as in work by Dohare et al., 2024, Abbas et al., 2023, and Lyle et al., 2023). Across all these fields, the basic spirit of plasticity is defined as follows:

Definition. (Plasticity, High-Level). Plasticity is the capacity of an input-output system to adapt.

We emphasize the input-output system here allows us to range over both bioligical organisms, as intended by James and Wheeler, but also artificial systems described in AI and cybernetics. Naturally, the notion of "adapt" is a historically contentious term to define---we'll largely try to sidestep some of the nuances of this debate by accommodating both a behavioral and cognitive notion of adaptivity. Roughly, a behavioral view says an agent adapts when its action choice meaningfully changes due to experience, while a cognitive view says an agent adapts when aspects of its cognition (beliefs, memories, parameters) meaningfully change due to experience. We'll center around the behavioral account, but both views can be captured by our definition.

Empowerment

Empowerment was first proposed by Klyubin et al. as "how much control of influence an [agent] has", with the term of course reflecting the intuition about how much "power" a system possesses. In this way, empowerment characterizes how much an agent can do in its world. Klyubin et al. emphasize it is an agent-centric quantity in the sense that empowerment is ultimately a property of an agent, rather than a property of the environment. Naturally, empowerment definitions often invoke both agent and environment to ask: how empowered is this agent, in this environment? Empowerment has been embraced and studied across a variety of subfields of AI, with a long line of work led by Polani and his group building the foundations. Collectively, the spirit of empowerment is defined as follows:

Definition. (Empowerment, High-Level). Empowerment is the capacity of an input-output system to steer.

In the case of a caterpillar (pictured above), the plasticity of the caterpillar refers to the extent to which the caterpillar can adapt based on new experience. For instance, it might see a fire, or a predator such as a bird, or a flower to climb: in light of these new stimuli, how can the caterpillar react? If it is capable of altering itself in some manner, either via its beliefs, memories, or behavior, we say the caterpillar is plastic. If, on the other hand, the caterpillar is unmoved by these observations in the sense that it would keep doing exactly what it would have had it not seen those observations, then we say the caterpillar has no plasticity. Conversely, the caterpillar's empowerment refers to how much it can influence what it experiences in the future through its action. If the caterpillar, through action, can reach a new leaf, or transform into a butterfly, which brings about even further diverse experiences, we say the caterpillar is empowered.

2. Formal Setup: Agents and Information (top)

To make our definitions of plasticity and empowerment mathematically precise, we build around some simple ingredients. The starting point is to assume we have already agreed on the space of inputs defined by the finite set \(\mathcal{O}\) that we call the observations, and the space of outputs defined by the finite set \(\mathcal{A}\) that we call the actions. Then, together, these allow us to consider the set of sequences of actions and observations that could form when an agent interacts with an environment using this interface. In total, here is a simplified version of the basic elements:

So, our agent is a stochastic function that maps each history to a distribution over actions, and our environment is a stochastic function that maps each history to a distribution over observations. Together, an agent \(\lambda\) and an environment \(e\) that share an interface can interact by exchanging observations and actions back and forth, forming the stochastic process \(A_1 O_1 A_2 O_2 ... A_t O_t ...\) involving discrete random variables \(A_i, O_i\). We won't fuss too much over whether the agent or environment emits first: we believe this is ultimately benign.

From these ingredients, Klyubin et al. define empowerment using information theory, as follows:

Definition. (K-Empowerment). For any \(n \in \mathbb{N}\), the n-step K-empowerment of an agent \(\lambda\) in an environment \(e\) is defined by \(\mathfrak{E}^n(\lambda, e) = \max_{p(a^n)} \mathbb{I}(A_{1:n}; O_n)\).
Let's unpack this definition, as there are a few things going on. First, \(\mathbb{I}(A^n; O_n) \) refers to the mutual information of the sequence of n actions with the observation that follows them. Intuitively, this quantity is high when an observer, on learning actions \(A_{1:n} = (A_1, A_2, ..., A_n)\), also learns a great deal about the subsequent observation, \(O_n\). In this way, this reflects that agents ability to shape the observation after \(n\) steps. Now, the max is taken to reflect the agent's maximum potential to shape future observations---this turns the quantity into a channel capacity. If we remove the max, and simply consider the empowerment of just the function \(\lambda\), this is more in line with the "actual" empowerment, as pointed out by Capdepuy in their 2011 thesis. As also pointed out by Capdepuy, there are a few limitations to the above definition: First, that the max is taken over pmfs over action sequences, meaning that the action-selection strategies do not take feedback into account along the way. Second, that the quantity is relative to a single fixed \(n\), and must start from the beginning of time. To remedy these issues, we turn to Marko's Bidirectional Communication Theory.

Marko and Massey: Bidirectional Communication

In the 1970s, Marko generalized Shannon's original information theory in the following sense: In Shannon's setup, A sender (Alice) emits a signal across a noisy channel to a receiver (Bob). In Marko's theory, Bob can also emit a signal back to Alice, which can inform Alice's future signals, thereby creating an indefinite cycle of communication between the two. One of the main tricks in our paper is to draw an equivalence between Marko's bidirectional notion of communication and the interaction between agent and environment. That is, an agent and environment effectively communicate back and forth by exchanging action and observation symbols indefinitely.

Now, on Marko's theory, there are two signals of interest: \(X\), sent by Alice to Bob, and \(Y\), sent by Bob to Alice. And of course, we can repeat this process indefinitely, yielding the sequences of discrete random variables \(X_{1:n} = (X_1, X_2, ..., X_n)\) and \(Y_{1:n} = (Y_1, Y_2, ..., Y_n)\). Naturally, each \(Y_i\) can depend on all the signals that came before (both \(X_{1:i}\) and \(Y_{1:i-1}\)).

In the 1990s, Massey pointed out that in Marko's setup, there are really two kinds of information: first, the information sent from \(X\) to \(Y\), and second, the information sent from \(Y\) to \(X\). Massey called defined these two using the directed information, as follows.

Definition. (Directed Information). The directed information from \(X_{1:n}\) to \(Y_{1:n}\) is defined as
\(\mathbb{I}( X_{1:n} \rightarrow Y_{1:n}) = \sum_{i=1}^n \mathbb{I}(X_{1:i}; Y_i \mid Y_{1:i-1})\).

The really neat thing about directed information is that we can immediately relate it to regular mutual information. Massey and Massey in the 2000s proved what they call a "conservation law" of information, showing that the mutual information between all signals emitted by Alice and Bob is the sum of the two directed information terms:

Theorem. (Massey and Massey, 2005: Conservation Law of Information).
\(\mathbb{I}(X_{1:n} \rightarrow Y_{1:n}) + \mathbb{I}( Y_{1:n} \hookrightarrow X_{1:n}) = \mathbb{I} (X_{1:n} ; Y_{1:n})\),
where the \(\hookrightarrow\) is used to account for off-by-one/fence-post issues.

What this means is that if Bob never sends any messages to Alice, the total information is just the directed information from Alice to Bob. The above theorem is a way to decompose the total information into their two respective sources: in this way, it is invoking some concepts closely related to causality, though is less powerful than a full causal language.

3. Generalized Directed Information (GDI) (top)

One restriction of the directed information is that it is only well-defined for sequences that begin at the start of time, and range over the same length \(n\). However, empowerment and plasticity as concepts are meaningful throughout an agent's lifetime. In fact, we should be able to ask about an agent's empowerment over any window of its experience. It is meaningful to ask about the evolution of an agent's plasticity throughout its experience (this is precisely what underlies the intuition that plasticity can be "lost" over time!). For this reason, we next turn to enriching the definition of directed information.

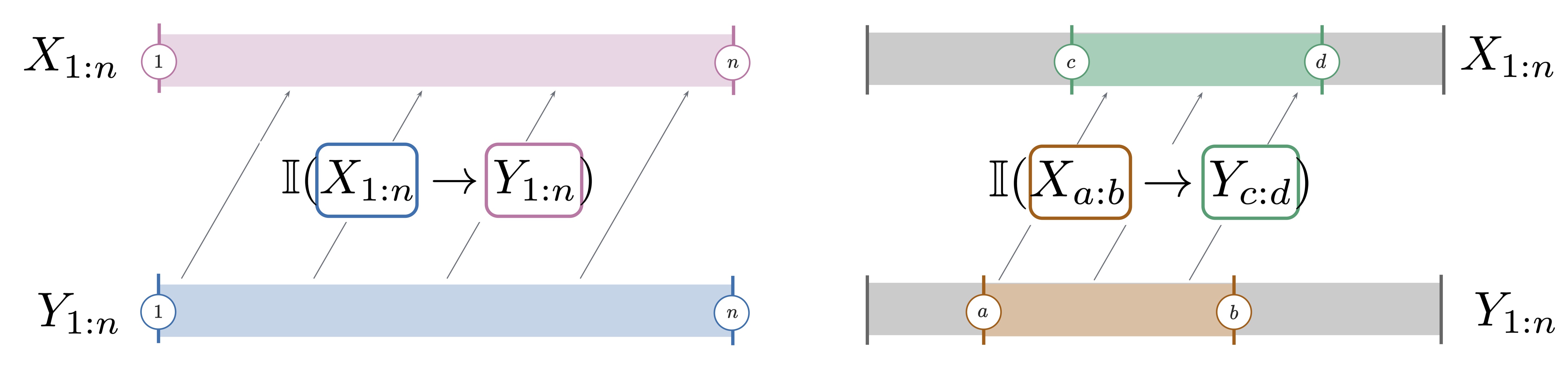
Intuitively, what we end up with is pictured above: We introduce a generalization of the directed information that allows us to pick both the preceding interval (for the variable \(X\) on the left) and the latter interval (for the variable \(Y\) on the right). Formally, we define this as follows.

Definition. (Generalized Directed Information). The generalized directed information from interval \([a:b]_n\) to \([c:d]_n\) is
\(\mathbb{I}(X_{a:b} \rightarrow Y_{c:d}) = \sum_{i=\max(a,c)}^d \mathbb{I}(X_{a:\min(b,i)}; Y_i \mid X_{1:a-1}, Y_{1:i-1})\),
where \([a:b]_n\) refers to any interval where \(1 \leq a \leq b \leq n\).

So, for any bidirectional communication setup, we can then ask about the GDI between any two subsequences: For instance, \(\mathbb{I}(X_{3:5} \rightarrow Y_{2:20})\), measures the influence from \(X_3, X_4, X_5\) on \(Y_2, Y_3, ..., Y_{20}\).

How do we know we have captured this definition properly? Well, we prove a few intuitive properties that allow us to conclude this is a valid extension of the directed information. As a quick summary:

We visualize the fourth bullet below:

Intuitively, the above means we can always decompose (along either the left variable or right variable) an interval and retain the same total amount of information flow. The same intuition underlies the extension of the conservation law:

Theorem. (Conservation of GDI). For any \(n \in \mathbb{N}\) and valid intervals \([a:b]_n\) to \([c:d]_n\)
\(\mathbb{I}(X_{a:b} \rightarrow Y_{c:d}) + \mathbb{I}( Y_{c:d} \hookrightarrow X_{a:b}) = \mathbb{I} (X_{a:b} ; Y_{c:d} \mid X_{1:a-1}, Y_{1:c-1} )\),

This result extends and generalizes the above theorem of Massey and Massey for directed information: Notice that if \(a=c=1, b=d=n\), we recover the same exact theorem. We are really excited about the GDI as a general purpose tool for the many fields that make use of information. For more analysis and details, see Section 3 of the paper.

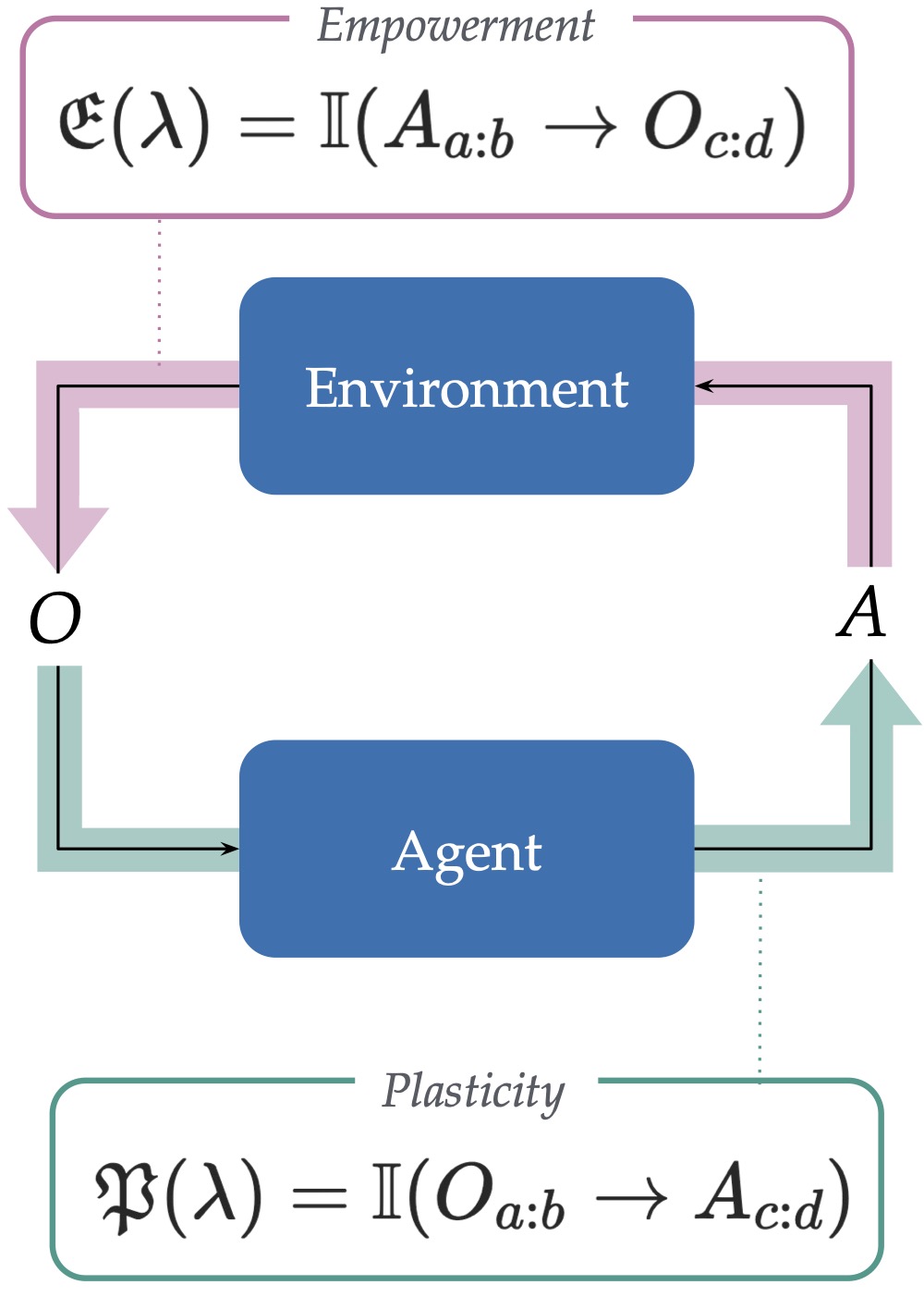
4. Main Results: Plasticity-Empowerment Tension (top)

Now, we get back to the main thread: the plasticity and empowerment of an agent. We saw before that Klyubin et al. defined empowerment using mutual information. We are here embracing this perspective, only we advocate for the GDI as a useful way to capture both plasticity and empowerment, as follows. In all cases, we assume we deal with an agent and environment that share an interface.

Definition. (Plasticity). The plasticity of agent \(\lambda\) in environment \(e\) from \([a:b]_n\) to \([c:d]_n\) is
\(\mathfrak{P}(\lambda, e) = \mathbb{I}(O_{a:b} \rightarrow A_{c:d})\).
Definition. (Plasticity). The empowerment of agent \(\lambda\) in environment \(e\) from \([a:b]_n\) to \([c:d]_n\) is
\(\mathfrak{E}(\lambda, e) = \mathbb{I}(A_{a:b} \rightarrow O_{c:d})\).

Theorem. (Plasticity-Empowerment Tension).

5. Discussion (top)

6. Reflections and Anecdotes (top)

7. Further Reading (top)

All Posts