David Abel

Portrait


Silly Game 3.0: Zippable Words

09/01/2019

I'm back with another goofy little word game (see previous installments here and here). This time, I explore the prevelance of word pairs with the structure illustrated by the following image (more from the reddit post here):

After I saw this, I was curious about word pairs of this kind. In particular, I started thinking about the following questions: how many other word pairs exist in the standard English language that could be stitched together to create graphics of this form? What are the longest such pairs? To make things concrete, let's define the specific property as follows:

Definition (Teach Peace Property): The Teach Peace property is said to obtain of a word pair \(w_1, w_2\), if \(len(w_1) = len(w_2)\), and there is some prefix/suffix length \(n\) such that \(0 < n < len(w_1) \) where the following three hold:
  1. (Diff prefix): \(w_1[:n] \neq w_2[:n]\)
  2. (Diff suffix): \(w_1[-n:] \neq w_2[-n:]\)
  3. (Same middle): \(w_1[n:-n] == w_2[n:-n]\).

Per the image above, the Teach Peace property says that two words are the same length, have different suffixes/prefixes (of the same length), but share characters in the middle of the word (of the same length). Of course there are many such short words: (can, bat), (tin, hit), and so on. However, it is a bit harder to come up with longer words that satisfy the property.

I was curious (as with the other word games) about the longest such pair, and the general density of satisficing word pairs amongst different corpora. I put together some code to play around with these questions. I didn't find any pairs that were quite as satisfying (semantically) as teach-peace, but I found a few. First, let's look at a few interesting (relatively long) satisfying word pairs for the usual word list (the 3000 most common words in English):

  1. (burden, murder)
  2. (attention, potential)
  3. (infection, effective)

And a few groups of words that are all inter-satisficing (that is, they define large equivalence classes):

  1. (operate, overall, average, therapy)
  2. (italian, qualify, quality, realize, reality)
  3. (russian, session, massive, passion, mission, missile)
  4. (adventure, attention, incentive, scientist, intention, potential, essential)
  5. (impressive, depression, expressive)

The largest equivalence class (for words of length four or greater) was seven ('adventure', 'attention', ...).

I next visualized the density of the total number of satisficing pairs of different lengths. As with many phenomena in natural language, the distribution ends up being Zipf-like, both for the common words corpus and Alice in Wonderland corpus:

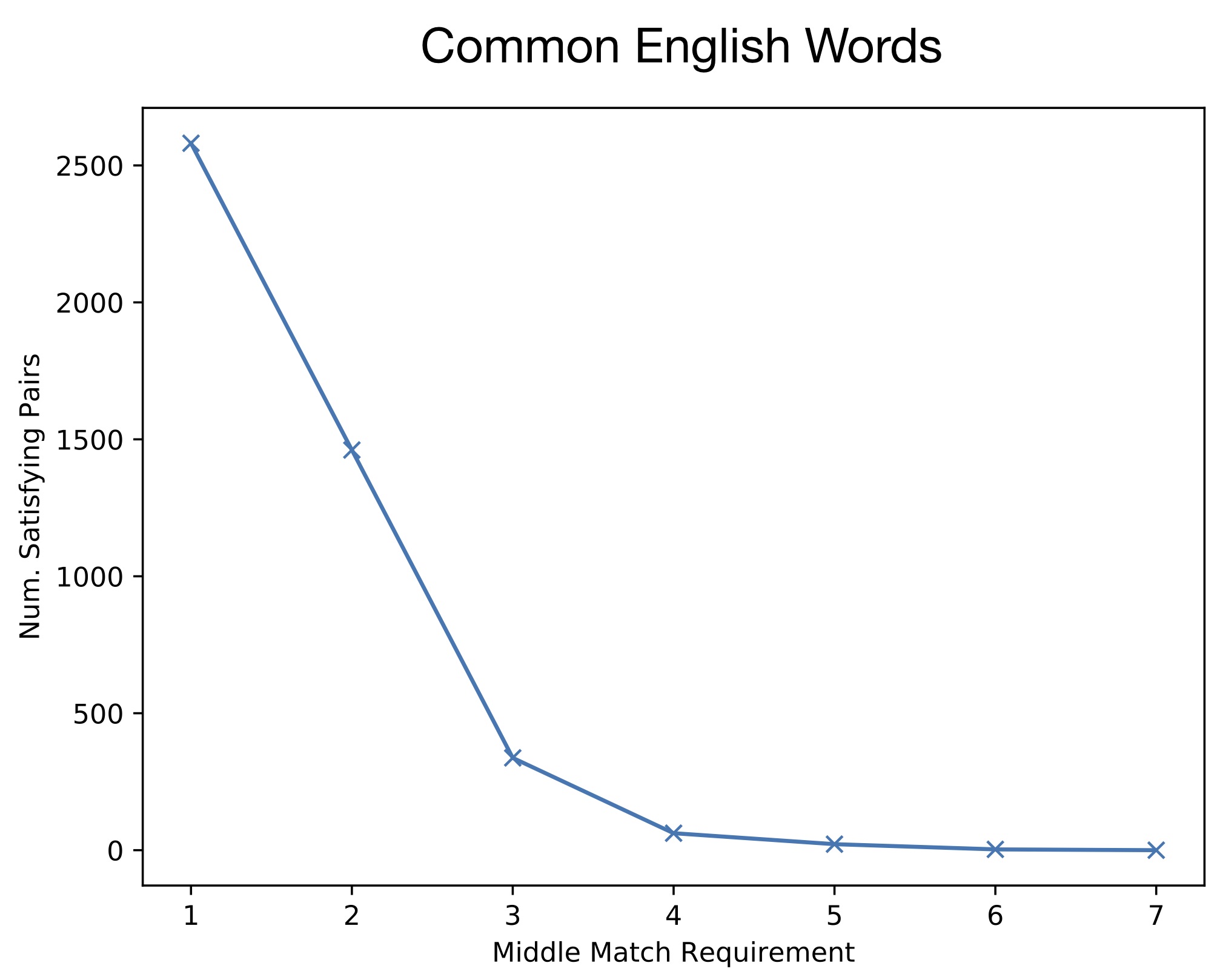
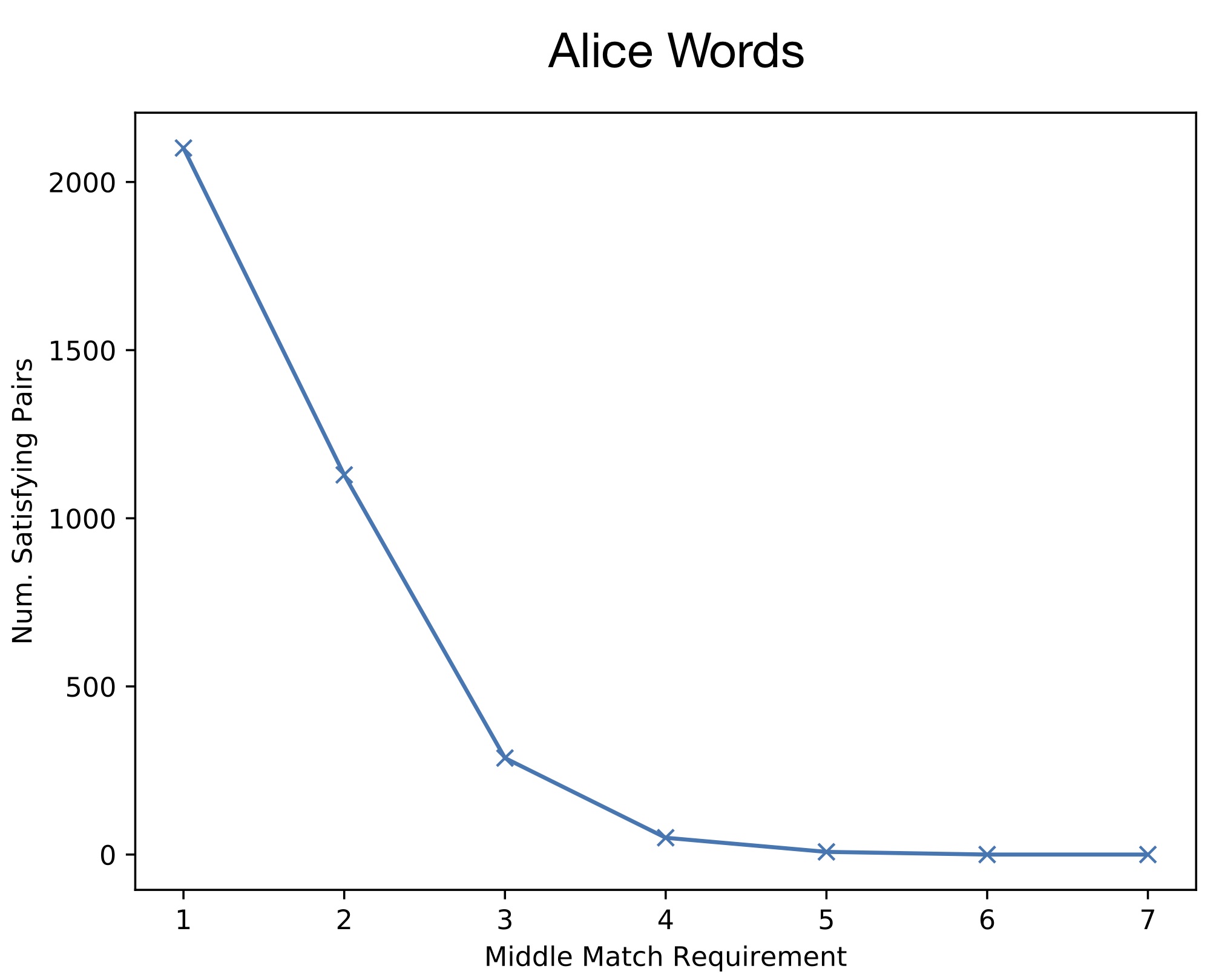
So, in the above plots, the x-axis denotes the number of matching letters between word pairs. So, for instance, "eat" and "car" would have a match length of one, while "teach" and "peach" have a match length of three. Given each corpus, the above plots show how many total words there are that satisfy the teach-peace property for each length.

As mentioned, the code is available in case you would like to play around with this property as well. Plenty of follow up things to try out: for instance, automatically generating images like the above given a satisficing word pair, or inspecting the relative ratio of teach-peace words compared to word-pairs that share any subset of n letters.

Cheers!

-Dave