David Abel

Value Preserving State-Action Abstractions

Today, I am joined by my collaborators Nathan Umbanhowar, Khimya Khetarpal, Dilip Arumugam, Doina Precup, and Michael L. Littman who recently co-authored Value Preserving State-Action Abstractions, to be presented this week at (virtual) AISTATS 2020. In this post, we present a broad overview of the work, highlighting the main contributions and providing some reflections on the methodology and results.

To summarize the paper in one sentence: we identify the kinds of state, action, and hierarchical abstractions that preserve representation of near-optimal policies in finite MDPs, as illustrated in the following image.

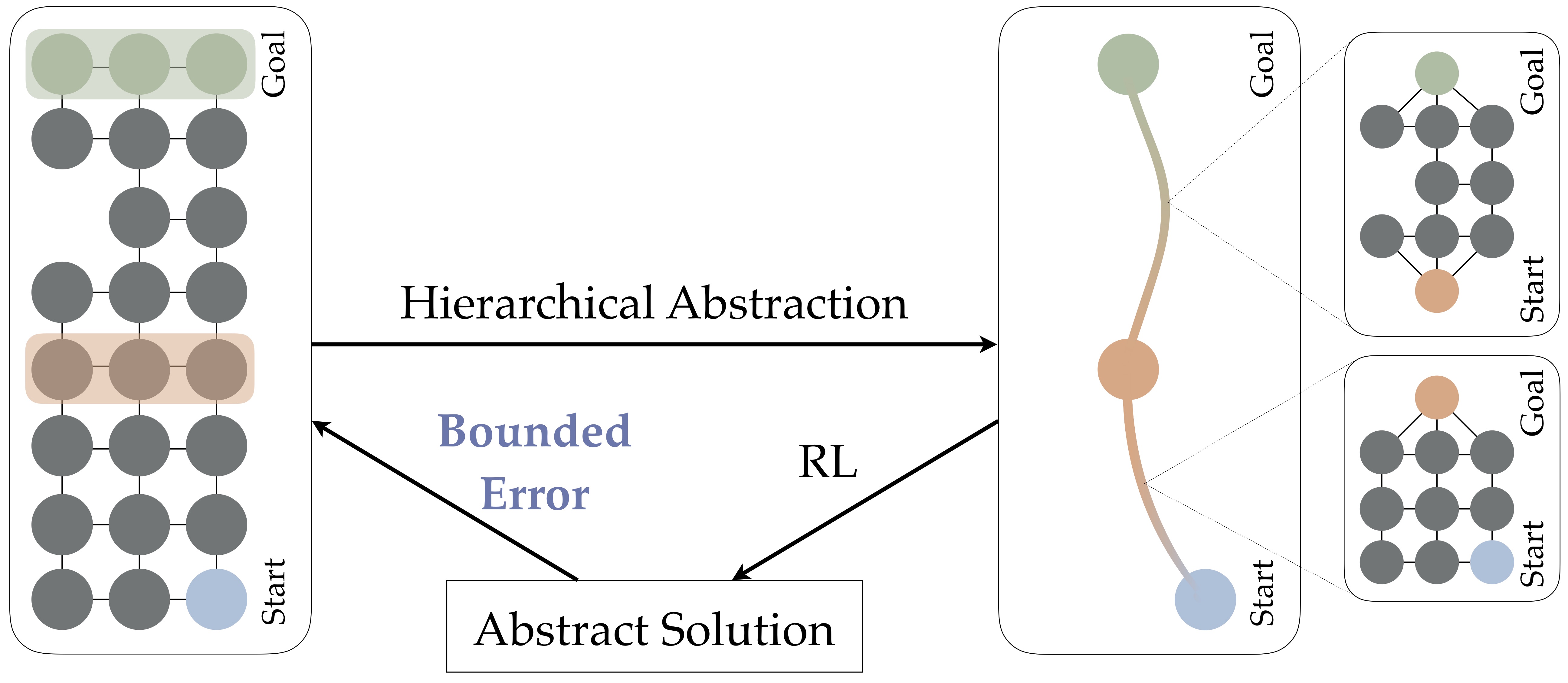
Feel free to reach out over email if you have further questions about the work!

Motivation

The focus of this work is on understanding the role that the process of abstraction could play in reinforcement learning (RL). For some background on abstraction in RL, see an earlier post on our 2018 ICML work here, or an overview of some recent literature in a more recent post.

Broadly, abstraction is the process of simplifying an entity. When that entity is a complex world, and an RL agent inhabits that world, abstraction is the process responsible for translating an agent's stream of observations into a compact representation that informs decision making. Mark Ho recently pointed me to the short (one paragraph!) story by Jorge Luis Borge called On Exactitude in Science, in which map makers discuss the appropriate scale for a map of their country. They ultimately settle on a map that uses a 1:1 scale---but, sadly, the map is prohibitively large (as big as the country!), so they just use the country itself instead. This story identifies the fundamental tension at play with abstraction; it must create a pliable, useful, but compact representation.

In MDPs, there are two natural forms of abstraction. A state abstraction is a function that changes the state space of the agent, and an action abstraction is a function that changes the action space of the agent. Concretely, we will adopt the following definitions:

An RL agent can then incorporate a state and action abstraction into its learning process as follows. First, when the MDP outputs a state \(s\), the agent passes it through \(\phi\), yielding the abstract state \(s_{\phi}\). The agent then performs any learning updates, then outputs an action by selecting among the available options in the given state, \(\Omega(s_{\phi})\), denoting the option set \(\Omega(s_{\phi}) \subseteq O\) that initiate in \(s_{\phi}\). The chosen option \(o\) then commits to its policy \(\pi_o\), outputting each ground action \(a \sim \pi_o(s)\). This process is visualized in the traditional RL loop as follows.

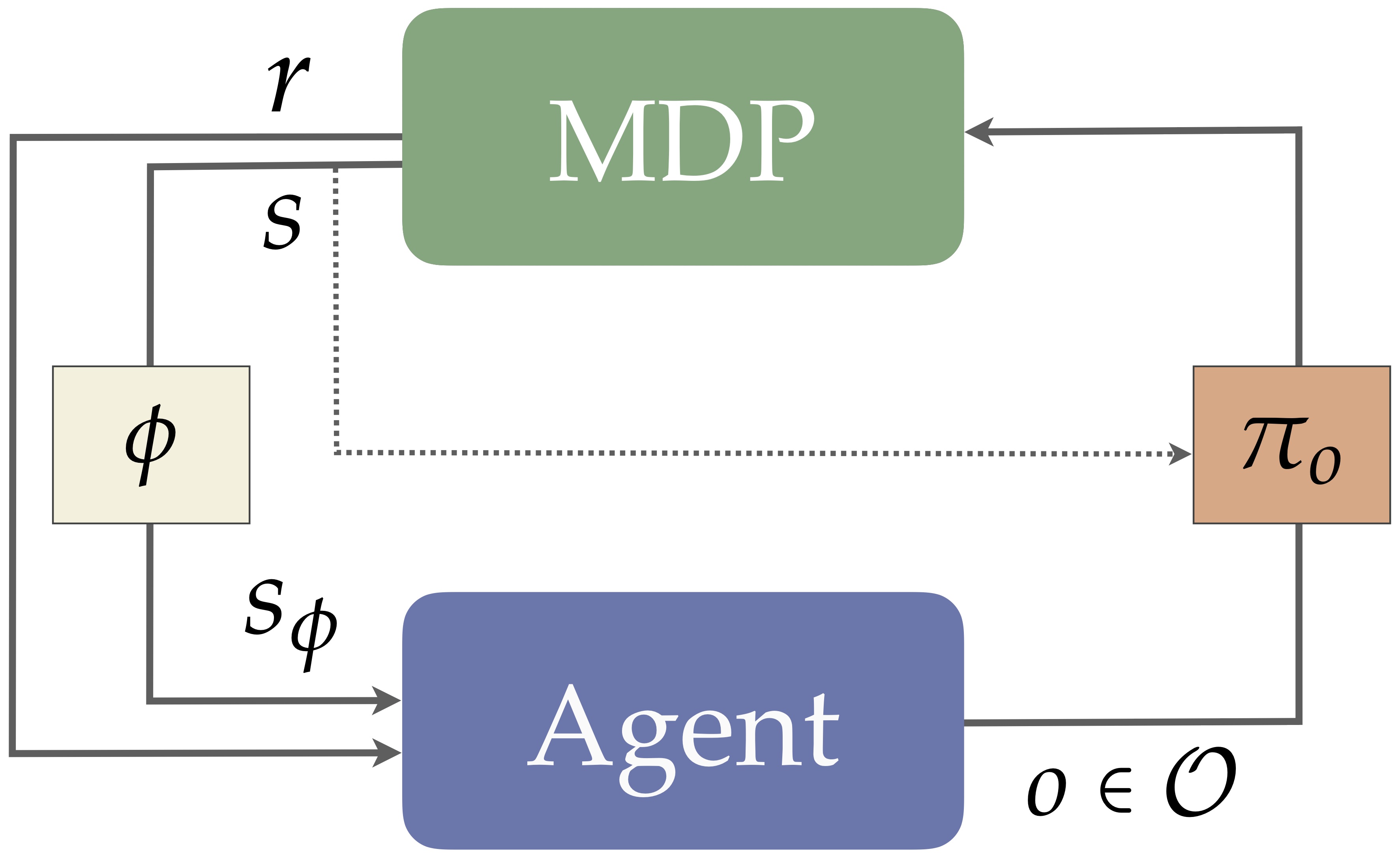
With these pieces in play, a natural question arises: Which function \(\phi\) and which option set \(O\) should an RL agent use? At a high level, we adopt the perspective that abstractions should, at the very least, allow agents to represent good behavior. That is, at some point, even if an agent had unlimited experience or computational resources, the abstractions should permit the discovery of satisfactory behavioral policies. Naturally there are other properties one might care about, but this is certainly one desirable property of abstractions. For more discussion on the kinds of properties we might hope abstraction adheres to, see chapter 2 of my dissertation. Concretely, this paper asks and answers the following question:

A long line of work (see earlier post for an overview of the ) focuses on understanding which kinds of abstractions preserve representation of good behavior. This work is expansive, covering topics in state abstraction (see work by Whitt, Even-dar and Mansour, Van Roy, Li, Walsh, and Littman, Hutter, and Majeed and Hutter), model minimization (see Dean and Givan, Ravindran and Barto 1, 2, 3, or Ravindran's dissertation), model selection (see Ortner et al. 1 and 2, Jiang et al.), state metrics for MDPs (see work by Ferns et al. 1 and 2 and Castro), combinations of state-action abstraction (see Bai and Russell), and hierarchical abstraction (see work by Nachum et al.). We build on these works by concentrating specifically on value loss bounds when state and action abstraction are both used. For more on background on these and related works, see Chapter 2 of Dave's thesis (and specifically section 2.2.1 and section 2.3.1)

We build on this work in this paper by offering two new general results that clarify which kinds of abstractions preserve representation of globally near-optimal policies:

1. Theorem 1: There are four classes of joint state-action abstractions that still preserve representation of near-optimal policies.
2. Theorem 2: We can construct hierarchies out of these state-action abstractions that ensure the hierarchy can also represent near-optimal policies (subject to two crucial assumptions about the hierarchy's construction).

The remainder of the post will build up our main results. First, we introduce the four classes of state-action abstractions and present our first main result. Then, we describe how to construct hierarchical abstractions from state-action abstraction primitives and present our second main result.

A Simple Recipe for State and Action Abstraction in MDPs

First, we will need a mechanism for analyzing the kinds of policies that a given state-action abstraction can represent. Arguably, in retrospect, figuring out how to do this appropriately was one of the main insights behind the work.

So, roughly, we are given some state abstraction \(\phi\) and a set of options such that, for every abstract state, there is at least one option that initiates in that abstract state, and every option terminates when its option policy leaves the abstract state it started in. This ensures that there is always one option available to the agent, no matter which environmental state the agent arrives in. It also ensures that every abstract policy over \(s_{\phi}\) and \(o\) will map to a unique Markov policy over ground states and actions. That is, we may think about \(\phi\) and \(O\) as carving out a region of representable policies:

We adopt the double arrow superscript notation to denote this grounding process. This double arrow policy is sure to exist due to the folllowing transformation of any abstract policy. That is, for any abstract policy that takes \(s_{\phi}\) as input and outputs some \(o\), we can translate it into a policy over \(s\) and \(a\) as follows.

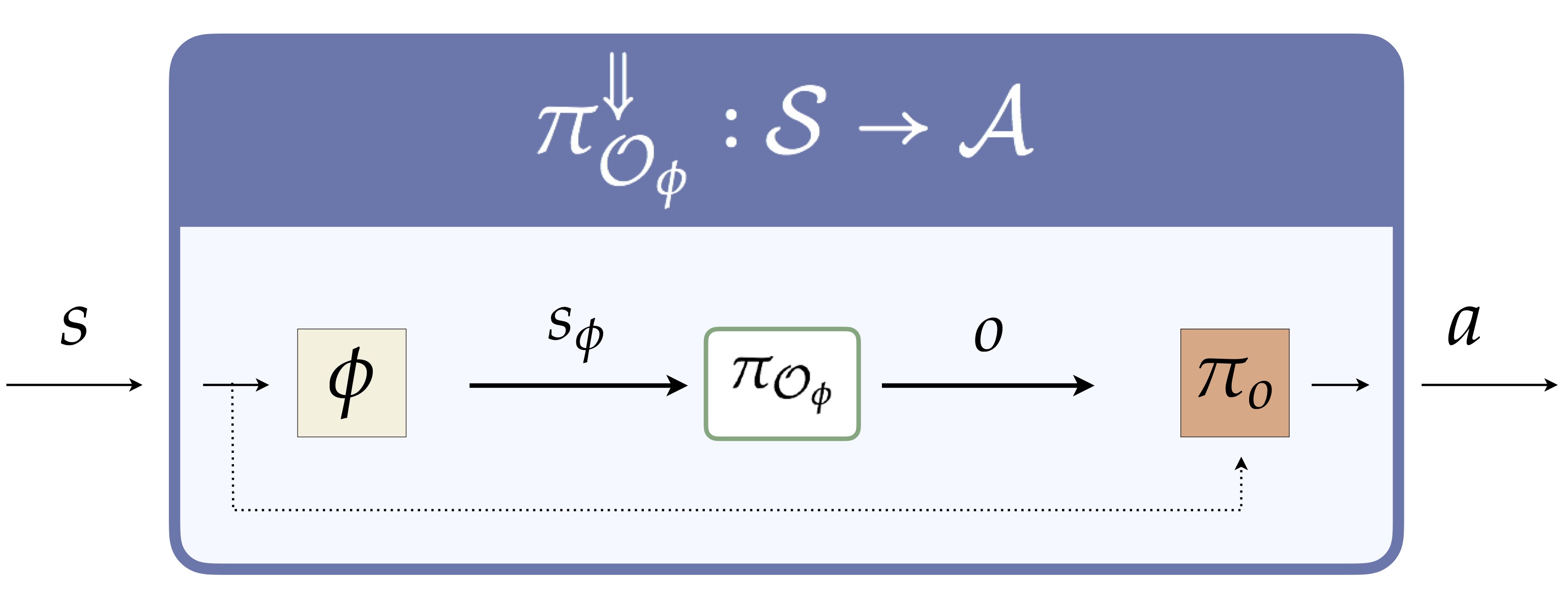
With this perspective in place, we can now state formally how to evaluate the quality of the policies representable under a given \(\phi\) and \(O_{\phi}\) pair. Our results will then tell us how to ensure the beige bubble above is guaranteed to contain at least one near-optimal policy.

Given a state abstraction \(\phi\) paired with a set of \(\phi\)-relative options, to study theoretical guarantees, it is of our interest to define and measure the degree of suboptimality one might incur in such a scenario. Value loss is therefore defined as the maximum difference in the value function between the optimal ground policy and the best policy representable by \(\phi\)-relative options. In other words, it is the smallest degree of sub-optimality achievable by the \(\phi\)-relative options.

Notably, this definition intently restricts attention to \(\phi\)-relative options. This is unique in the sense it allows each \(\phi\)-relative option to retain structure that couples with the corresponding state abstraction \(\phi\) to yield value functions in the ground MDP.

It is worth noting that the \(\phi\)-relative options as presented above begin with a particular choice of state abstraction, \(\phi\), and then induce a natural action abstraction based on \(\phi\). In this work, we will focus on this particular recipe although a perfectly suitable alternative would be to start off with a particular set of options or skills and then induce a corresponding state abstraction which support those provided skills. This latter style of approach has been well-studied by George Konidaris and does admit its own kind of theoretical guarantees (see this paper for a broad overview of this directionality and this paper for more details).

Main Result 1: Value Preserving State-Action Abstractions

With these tools in place, we now move on to our first main result.

We have already defined value loss to be the maximum difference in value between the best policy representable by our \(\phi\)-relative options and the optimal policy. Our key insight in definining the four option classes with bounded value loss is that the overall value loss can be decomposed according to the value loss per abstract state. Letting \(o^*_{s_\phi}\) denote the option which initiates in \(s_\phi\) and executes the optimal policy, we can define our first option class:

Loosely, this option class declares that each abstract state contains an option which is in some sense useful, to degree \(\varepsilon_Q\). In our paper, we show that by chaining these options together across abstract states, an agent can represent a policy with value loss that is bounded by \(\frac{\varepsilon_Q}{1-\gamma}\).

Two more option classes with bounded value loss follow as subclasses of this result.

This class ensures that an option is present in each abstract state which behaves in a locally optimal manner. The local closeness in models implies closeness in Q*-values, and therefore induces a value loss bound of \(\frac{\varepsilon_{R} + |\mathcal{S}| \varepsilon_{T} RMax}{(1-\gamma)}\).

This class presents a slightly different version of locally optimal behavior, in which the termination probabilities are not discounted and summed over time, as they are in the multi-time model \(T_{s,o}^{s'}\). In goal-based MDPs, where reward is only provided upon reaching a goal state, we show that options in this class have a value loss bound of \(\frac{\tau \gamma |\mathcal{S}|}{(1-\gamma)^2}\).

Our final value-preserving option class links our work to Ravindran and Barto's (2004) work on MDP homomorphisms. In particular, we prove that a deterministic policy over a set of \(\phi\)-relative options induces a particular MDP homomorphism. We define this option class based on the quantities \(K_p, K_r\), which roughly describe the maximum discrepancy in transition and reward models between the ground and abstract MDPs (see the paper for a precise definition).

Leveraging the main result of (Ravindran and Barto, 2004), we are able to show that this option class has value loss bounded by \(\frac{2}{1-\gamma} \left( \varepsilon_r + \frac{\gamma RMax}{1 - \gamma} \frac{\varepsilon_p}{2}\right)\).

Main Result 2: Value Preserving Hierarchical Abstraction

Theorem 1 only focuses on a single level of abstraction. How does this result scale as the process of abstraction is repeated to form a hierarchical structure? Our second result addresses this question.

We consider hierarchies of a simple but general kind: a hierarchy is just a collection of state abstractions (how should state be represented at each level?) and a collection of action abstractions (how should I represent actions at each level?). Assuming there are \(d\) of each type, we call this a depth \(d\) hierarchy, visualized as follows.

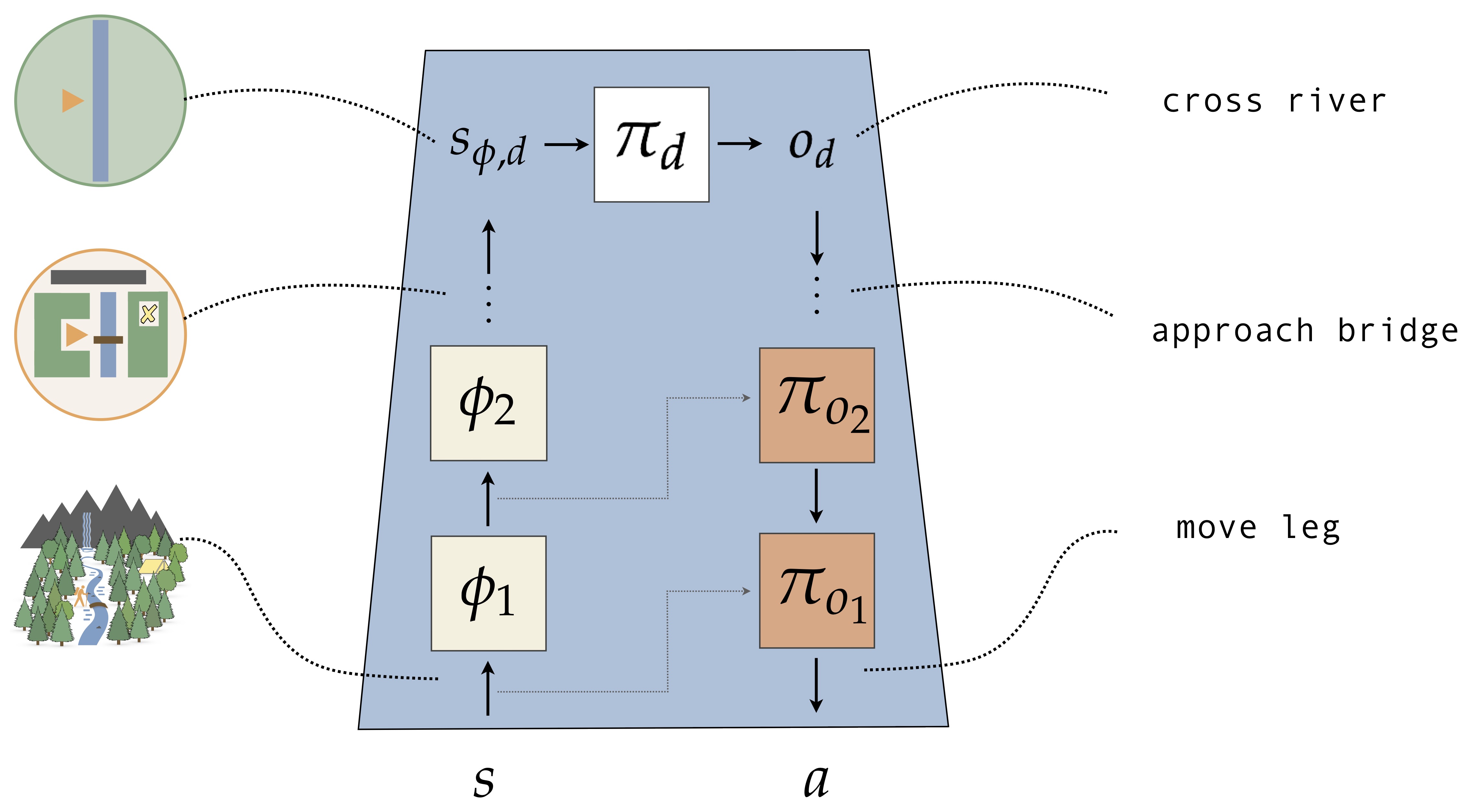
This structure can be transformed into the single abstraction RL form we saw previously:

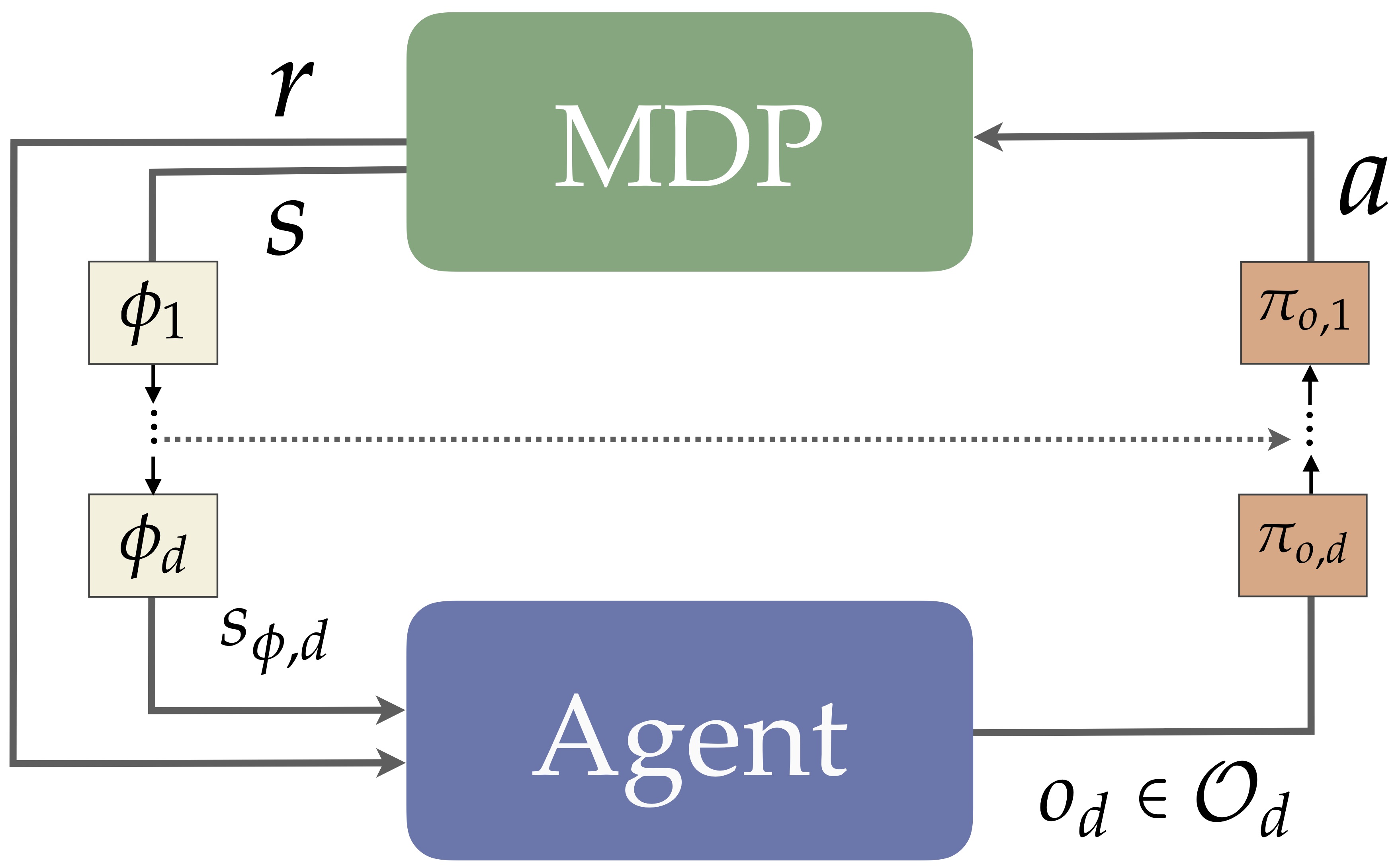
In other words, this form of hierarchical abstraction is agnostic to the learning algorithm (at least in its present form). As with a single pair \(\phi,O_{\phi}\), we again find a strategy for grounding a hierarchical policy to a ground level policy, too:

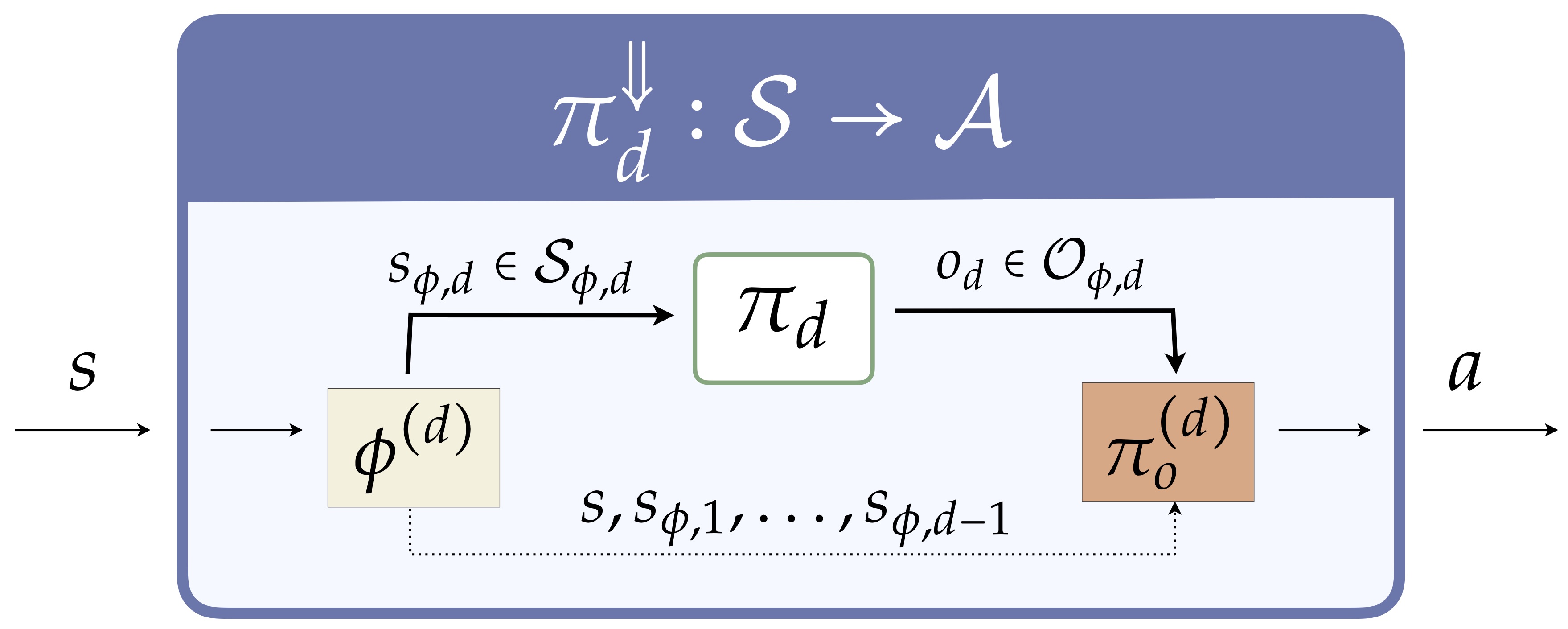
Since every hierarchical policy has a corresponding ground policy, we are then able to ask about the value loss of a hierarchy---how good is the best grounded policy? This again gives us a perspective of hierarchical abstraction as slowly limiting the policies representable.

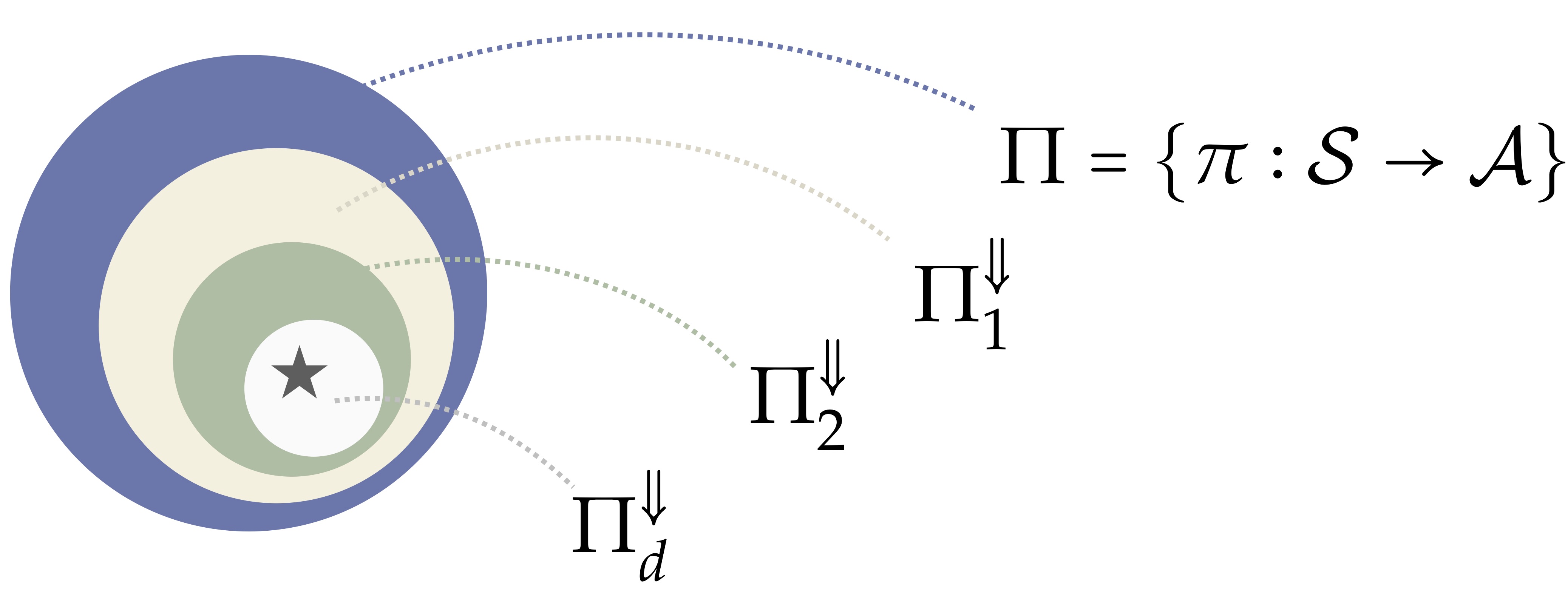
Which properties of a hierarchy must hold, at each level, such that the best policy at the top level is still pretty high in value? Note that crucially we are asking about the value of the hierarchical policy in terms of the value function of the original MDP---so, any claim about the optimality of a hierarchical policy in this form will be one of global optimality. Our result provides a statement of this kind.

The result relies on two assumptions about the hierarchy's construction:

1. Assumption 1: The value function representable up and down the hierarchy is similar.
2. Assumption 2: Subsequent levels of the hierarchy can represent policies similar in value to the best policy at the previous level.

The degree of loss depends on three quantities: 1) the loss in value expressivity (from Assumption 1), 2) the loss from policy expressivity (from Assumption 2), and 3) the depth of the hierarchy. To unpack the value-loss bound offered by Theorem 2, it is important to clarify our two assumptions.

The formal statement of Assumption 1 relates the value functions for a single policy at two adjacent levels of the hierarchy; intuitively, one can visualize this assumption as a claim concerning a single step up or down the hierarchy taken by the agent while learning or planning. As previously mentioned, abstraction is a tool for simplification and hierarchical abstractions endow agents with a multi-faceted view of the world at several degrees of simplicity. If, however, there is a substantial gap between the amount of simplification happening between two consecutive levels of the hierarchy, then the agent's knowledge at one level becomes less transferrable and is less representable at the next level. Assumption 1 guarantees that this is not the case and asserts that a value function computed at any level of the hierarchy has a counterpart at the level above and level below. Mathematically, it is the fidelity of this counterpart that ultimately appears in the value-loss bound of Theorem 2.

While Assumption 1 considers a single policy and examines the expressivity of value functions at adjacent levels of the hierarchy, Assumption 2 is concerned with comparing policies and examines our capacity to express a policy recovered at one level in the subsequent level. Recall that each level of the hierarchy can be seen as its own MDP with an associated policy class for mapping from states to actions. Assumption 2 simply asserts that the policy class of any level in the hierarchy is sufficiently expressive to represent a policy from an adjacent level. Consequently, a good policy found at a lower level of the hierarchy can be articulated at the next level up with bounded error. Just as before, it is the mathematical error in this translation between policy classes that ultimately appears as a term in the value-loss bound of Theorem 2.

Conclusions and Reflections

The main results of this work highlight which state-action abstractions are guaranteed to support the representation of at least one near-optimal policy. This degree of near-optimality is determined, in the worst case, by the amount of information that is used to inform the abstractions. Naturally, the \(\phi\)-relative option classes with the tightest bounds are those that depend on more extreme knowledge. The bounds in the second result also share this property, though there are three areas where the knowledge can shape the hierarchy: the similarity of the value functions expressible up and down the hierarchy, the similarity of the policies expressible up and down the hierarchy, and the hierarchy's depth.

Limitations. There are a number of limitations to these results to be aware of. First, as mentioned above, the abstractions depend on the presence useful knowledge about the environment. Often times folks are interested in acquiring abstractions and exploiting their usefulness before having to acquire valuable knowledge about the MDP of interest. This is indeed an important goal, though not one that we here focus on. An important extension might focus on the end-to-end discovery of such abstractions in a way that also makes use of them. Second, the two main results are focused on finite MDPs. They do not necessarily apply to infinite state or action spaces (though perhaps there is a natural extension of the results that would). Third, the option families we focus on are a peculiar subclass of options---they, along with the \(\phi\) they are relative to, can only specify policies that are contained in the originall policy space (\(\pi : S \rightarrow A)\)). However, a major source of power of options comes from their ability to express history-dependent policies in an otherwise Markov process. It may be natural to investigate such a class of options and whether they can preserve value too.

Reflections. In retrospect, this paper ended up being a mixture of work involving 1) setting up the state-abstraction and option interaction in the right way (so as to support a simple but useful value loss analysis), and 2) figuring out the right \(\phi,O_{\phi}\) classes to study (and their subsequent analysis), and 3) understanding the right way to extend these ideas to hierarchies. One conclusion that follows from Theorem 1 is that the quality of the state abstraction does not actually impact the value loss bound---instead, the representional quality is entirely determined by the options. However, the given state abstraction does shape the class of options available. In light of this, we speculate that an important role for state abstraction is to help control which areas of an environment are suitable for option discovery. That is, a state abstraction can help determine the learning difficulty for option policies. A second conclusion to draw from Theorem 2 is that hierarchical abstraction discovery algorithms may want to explicitly search for structures that satisfy Assumption 1 and 2: 1) value function smoothness up and down the hierarchy, and 2) policy richness at each level of the hierarchy. t each level of the hierarchy. In many ways this is reaffirming a natural insight from learning theory that has been known for a long time: more expressive hypothesis classes are more capable of explaining evidence. However, classical learning theory also tells us that simpler hypothesis classes are less likely to overfit, too, since there are fewer ways to explain the nuances of training data. In light of these considerations, we anticipate that hierarchies may want to be sensitive to a similar trade-off.

Thanks for reading! Let us know if you have questions --

Cheers,
--Dave, Nathan, Khimya, Dilip, Doina, Michael